The Symmetry of Space-Time Quanta

Table of Links

Abstract and Introduction

Space-time quanta and Becken Universal bound

Shape of space-time quanta

Symmetry of space-time quanta

Space-time quanta and Spectral mass gap

Phenomenological implications

Conclusion, Acknowledgments, and References

IV. SYMMETRY OF SPACE-TIME QUANTA

The symmetry group of 24-cell is the Weyl/Coxeter group of F4 group [40]. The 48 root vectors of F4 represent the vertices of the 24-cell in two dual configurations. F4 group is one of five exceptional simple Lie groups that are non-abelian and do not have nontrivial connected normal subgroups. The remarkable importance of the F4 group has been realized recently in [45] to explain the gauge symmetry of the standard model of particle physics. It is proved that F4 has two stabilizer groups that are H1 = (SU(3) × SU(3))/Z3 and H2 = Spin(9) that their intersection H1∩H2 generates the standard model gauge symmetry (SU(3) × SU(2) × U(1))/Z6. Further details and implications can be found in [46–58]. This supports our postulate of identifying the space-time quanta as the 24-cell. In addition, a geometric connection between 24-cell and Calabi-Yau Threefolds with Hodge Numbers (1,1) is realized in [59] that was useful in determining the mass spectrum of type-IIB flux vacua [60]. It is worth mentioning that 24-cell was crystallized to represent the spinfoam topology by trivalent spin network [61].

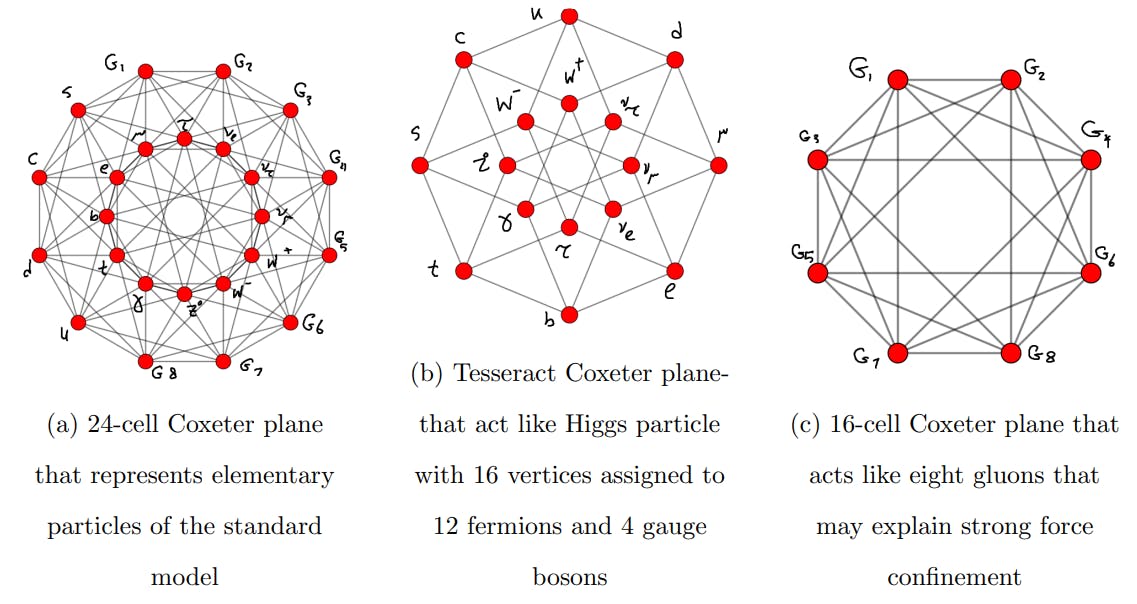
Let us now have a close look at Fig. (1) which shows a representation in a plane of 24-cell, where the vertices are divided into three subsets of three colors, each being a regular 16-cell. 24-cell vertices can be grouped into three different sets of eight vertices each one defining 16-cells with the rest defining the dual tesseract that has sixteen vertices [40]. These three different sets could be used to represent the three colors in quantum chromodynamics. Each set of eight vertices is represented by a 16-cell which is a regular convex 4-polytope that has eight vertices that can represent the eight gluons in the 24-cell. The other sixteen vertices of tesseract could be used to represent the twelve fermions and four gauge bosons. The tesseract is the four-dimensional analog of the cube. In that sense, the 24-cell can be formed by the 16-cell which could be assigned with eight gluons, and the tesseract which could be assigned with twelve fermions and four gauge bosons. Since the Higgs field couples only with the twelve fermions and four gauge bosons, therefore the tesseract as a whole could represent the shape of the Higgs particle. In addition, this property of 24-cell may explain the geometric meaning of preserving the gluons symmetry which may explain the color confinement. Besides, it explains why gluons could have three colors by grouping 24-cell vertices into three different sets of 16-cell as shown in Fig. (1). It also explains the flatness of the observable universe which is composed of 16 observable particles by the tesseract

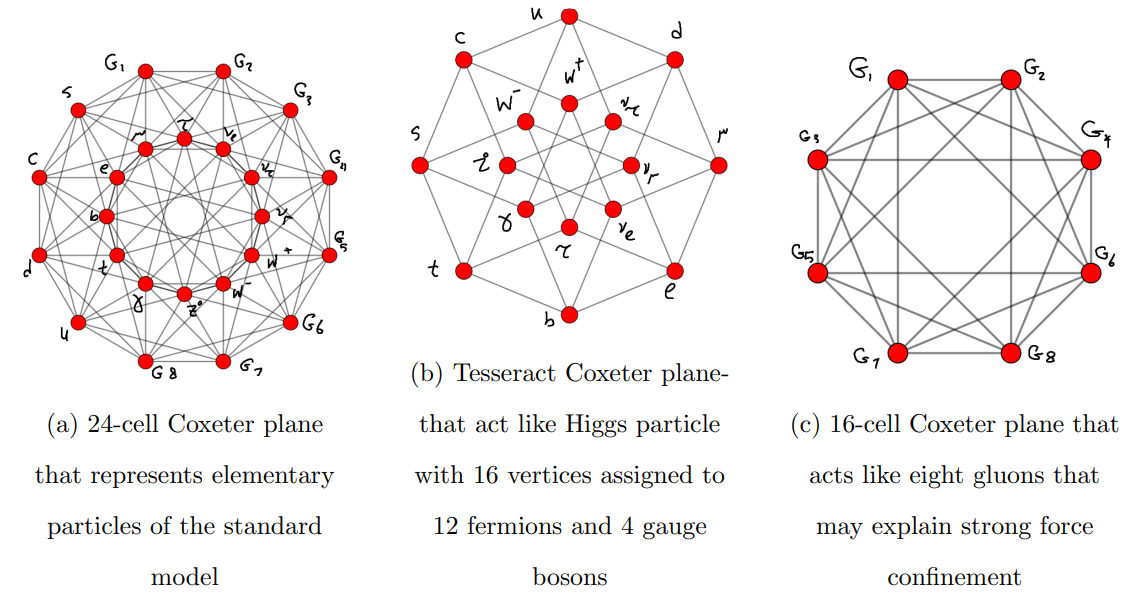
that has sixteen vertices and which is flat. We can represent the particles by orthogonal projections of 24-cell, 16-cell, and tesseract in the Coxeter plane in two dimensions as in Fig. (2).